Games of Chance vs. Games of Skill
A sufficient condition to detect a predominance of skill in a game (predominance test)
Jörg Bewersdorff
In most countries the regulations of gaming depend on the fact that the outcome of a game is predominantly influenced by skill or chance. In the past several proposals were given to measure skill in games (predominance test or predominant test).[9], [10]
In a paper, which I published in 2017 in a German legal journal[1] and in
an appended part of the 2nd edition of my book "Luck, Logic and Whitle Lies",[2] I presented an overview of laws, judgements, legal and mathematical literature on this topic. Some of these documents are dealing with proposals of a skill factor, which can partly interpreted as probability that a game is determined by skill (a summary is included in the presentation sheets[5] of my talk on 18 Nov 2019 at the University of Heidelberg and a Youtube video[6] of a webinar for the Concordia University, Montreal). Of course, for most games this factor isn't really a probability in a strict mathematical sense. Anyhow, it is possible to compare the success of low skill players and high skill players based on the relative frequencies of their success in a sequence of games.
The legal interpretation of the word skill is depending on jurisdiction. It may differ from state to state. But mathematics is an universal science. It is restricted to logical implications and helps to analyze reasoning. But there isn't any skill game in a mathematical sense, because a jurisdiction defines the context of playing the game and the meaning of a word does not matter in mathematics (David Hilbert explained axioms of geometry with the following words: "one must always be able to say, instead of 'points, straight lines, and planes', 'tables, chairs, and beer mugs'."). For example German jurisdiction requires to look for skill levels reachable by an average player.
In the mentioned papers I examined several simple games as case studies and benchmarks using insights based on game theory and statistics (two of these games are illustrated in the diagram below). As conclusion I presented a sufficient condition for a predominance of skill in a game.
In a first step the criterion is limited to the simple case of a symmetric two person game with only two outcomes +1 and -1. Such a game is predominantly skill influenced if the following sufficient condition is fulfilled: You can find two persons who a are both relevant in the legal sense (depending on the jurisdiction, which means for example in Germany that they are average players) where the better player has a probability of more than 0.75 to win a game. In this case the probability for an outcome decided by chance cannot be greater than 0.5, because each game which is decided by chance is won with probability 0.5 of each player.
The main idea of this sufficient criterion is very basic: The symmetry of the game can only strongly disrupted in average by the influence of the players. Similar considerations were alraedy made in the past, but it seems that there were some minor gaps in the argumentation concerning the restriction to symmetric games respective to the sufficient character of the criteria.[7], [8]
I presented similar criteria for other games, too: non symmetric games, games with several amounts of outcomes and games with more than two players. In the case of a tournament I computed the minimal number of games which is sufficient for a predominance of skill. An application to the game of poker is possible, but only based on a set of complete rules including a fixed poker variant like Texas Hold'em, betting limits, number of players and tournament rules.
Two mixed games as examples
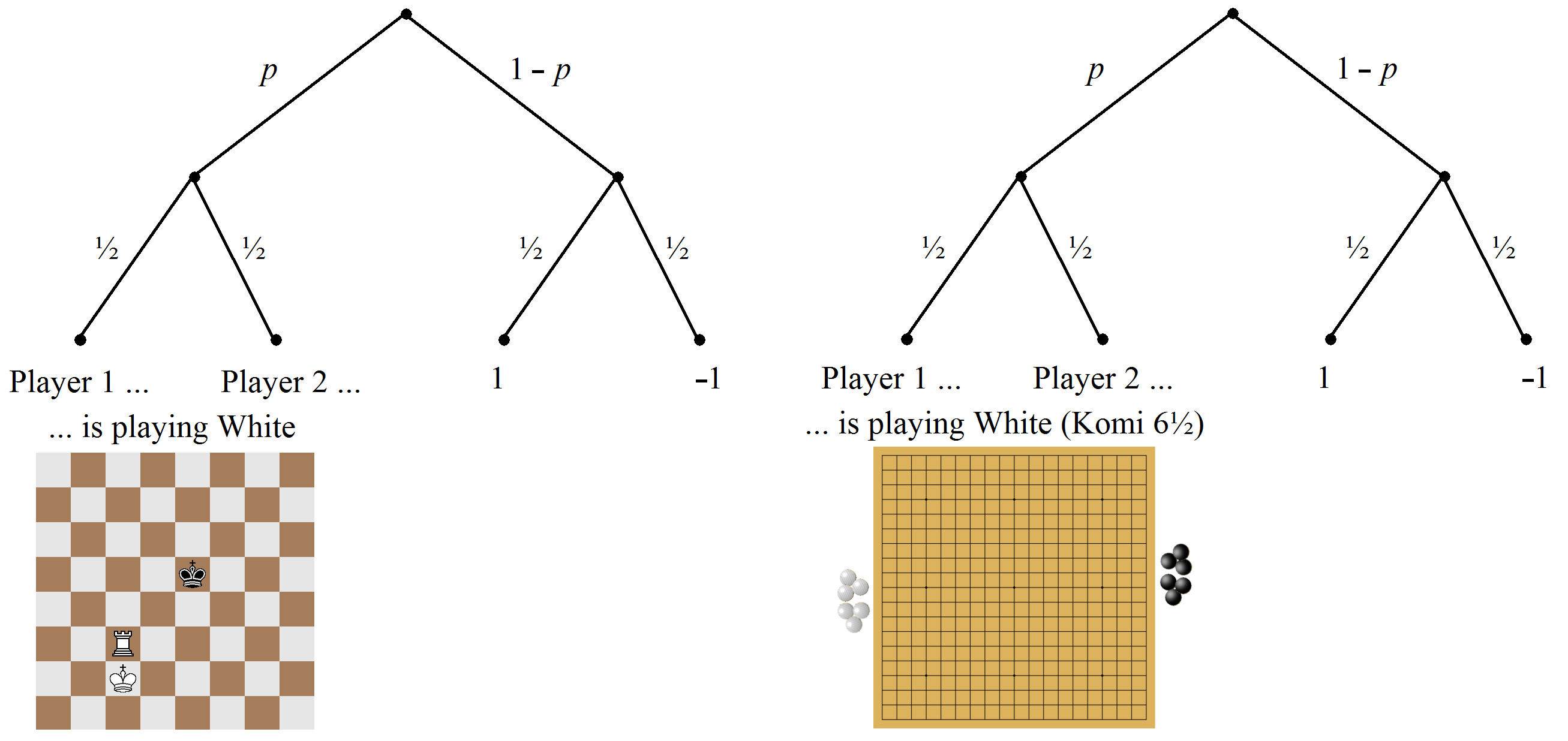
The diagram shows two symmetric two-person games, which are equivalent in the sense of their game-theoretical minimax analysis:
Each of these two games starts with two random moves depending on a fixed probability p. Depending on the results of these two moves the game terminates (probability for this: 1 – p) or continues by playing a subgame of pure skill (probability for this: p): a chess endgame king-rook-king (left game), respective a match of Go with komi 6½ (right game, a draw is not possible).
In the case of p = 0 both games are equal. The game is a pure game of chance.
In the case of p = 1 both games are consisting of a random decision of colors followed by a pure game of skill.
Most interesting is the case p = ½: The left game will be won by the player moving the white pieces. Therefore each player will win in 50 % of the plays, like in a symmetric pure game of chance. In the right game a player with more experience will win 75 % of the plays in average. In the case of p > ½ the game is predominated by skill.
|
References:
- Jörg Bewersdorff, Spiele zwischen Glück und Geschick, Zeitschrift für Wett- und Glücksspielrecht, 12 (2017), pp. 228–234, Open Access.
- Jörg Bewersdorff, Luck, logic and white lies: The mathematics of games, 2nd edition, Routledge 2021, ISBN 978-1-56881-210-6, DOI: 10.1201/9781003092872 as translation of Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7th edition, May 2018, ISBN: 978-3-658-21764-8, DOI: 10.1007/978-3-658-21765-5.
- Jörg Bewersdorff, DeepStack und rechtliche Implikationen, Zeitschrift für Wett- und Glücksspielrecht, 14 (2019), pp. 13–15, Open Access.
- Jörg Bewersdorff, Rezension von Thomas Bronder: Spiel, Zufall und Kommerz – Theorie und Praxis des Spiels um Geld zwischen Mathematik, Recht und Realität. 2. Aufl., 2020, Zeitschrift für Wett- und Glücksspielrecht, 15 (2020), pp. 403–404, Open Access.
- Jörg Bewersdorff, Skill and chance in games, presentation sheets of a talk, University of Heidelberg, 18 Nov 2019.
- Jörg Bewersdorff, (Distinguishing between) skill and chance in games, Youtube video of a webinar, MASSA Concordia (Mathematics, Actuarial, and Statistics Student Association of Concordia University, Montreal), 20 Jan 2021.
- Christian Laustetter, Die Abgrenzung des strafbaren Glücksspiels vom
straflosen Geschicklichkeitsspiel, Juristische Rundschau, 2012, pp. 507–513, DOI: 10.1515/juru-2012-0507.
- Rogier J. D. Potter van Loon, Martijn J. van den Assem, Dennie van Dolder, Beyond chance? The persistence of performance in online poker, PLoS ONE, 2015, 10(3): e0115479, DOI:10.1371/journal.pone.0115479 (Open Access).
- Marcel Dreef, Peter Borm, Ben van der Genugten, Measuring skill in games: several approaches discussed, Mathematical Methods of Operations Research, 59 (2004), pp. 375–391, DOI: 10.1007/s001860400347, (preprint: Open Access).
- Ingo C. Fiedler, Jan-Philipp Rock, Quantifying skill in games—theory and empirical evidence for poker, Gaming Law Review and Economics, 13 (2009), pp. 50–57, DOI: 10.1089/glre.2008.13106.
- Steven Heubeck, Measuring skill in games: A critical review of methodologies, Gaming Law Review and Economics, 12 (2008), pp. 231–238, DOI: 10.1089/glre.2008.12306.
- Anthony Cabot, Robert Hannum, Poker: Public policy, law, mathematics, and the future of an American tradition, T. M. Cooley Law Review, 22 (2005), pp. 443–514, online.
- Anthony N. Cabot, Glenn J. Light, Karl F. Rutledge, Alex Rodriguez, A monkey, and the game of Scrabble: The hazard of using illogic to define the legality of games of mixed skill and chance, Drake Law Review, 57 (2009), pp. 383-412, online.
- Steven D. Levitt, Thomas J. Miles, The role of skill versus luck in poker evidence from the World Series of Poker, Journal of Sport Economics, 15 (2014), pp. 31-44, DOI: 10.1177/1527002512449471, (preprint: Open Access)
- Michael A. DeDonno, Douglas K. Detterman, Poker is a skill, Gaming Law Review, 12 (2008), pp. 31–36, DOI: 10.1089/glr.2008.12105.
- Jakob Erdmann, Chanciness: Towards a characterization of chance in games, International Computer Games Association Journal, 32 (2009), pp. 187–205, DOI: 10.3233/ICG-2009-32402, preprint (Open Access). Extended version: Jakob Erdmann, The characterization of chance and skill in games, PhD thesis, Jena 2010, urn:nbn:de:gbv:27-20110513-132100-1 (Open Access)
- Peter Duersch, Marco Lambrecht, Joerg Oechssler, Measuring skill and chance in games, European Economic Review, 127 (August 2020), 103472, DOI: 10.1016/j.euroecorev.2020.103472, preprint: University Heidelberg, Discussion Paper, 643 (2017), DOI: 10.11588/heidok.00023867 (Open Access)
Some important judgments concerning skill and chance in games:
- United States:
- United States District Court, E.D. New York., U.S. v. Dicristina, case number: 1:11-cr-00414-JBW (21 August 2012), online (U.S. Government information):.
The court decided that poker is predominantly influenced by skill—not as single game but in sequence of games if this sequence is long enough. And this number of games “is easily reached by poker players in tournament play”.
- Germany:
- Reichsgericht (Imperial Court of Justice, Germany: from 1879 to 1945 the supreme criminal and civil court), judgment on 18 May 1928, case number: I 977/27, Entscheidungen des Reichsgerichts in Strafsachen, 62, pp. 163–173, online (original publication using Fraktur letters, transcript with latin letters):
The court compared the success of an average player using skill with the success of a randomly acting player. Also the operator, represented by a machine or a dealer, has to be seen as a second player who is winning without skill.
- Bundesverwaltungsgericht (Federal Administrative Court, Germany), judgment on 17 May 1955, case number: 1 C 133.53, (online):
The meaning of average player does not include a behavior based on complicated mathematical computations to get an optimal strategy. Crucial is only what is really played.
- Bundesverwaltungsgericht (Federal Administrative Court, Germany), judgment on 9 October 1984, case number: C 20.82, (online):
The predominance of skill or chance in a game must be analysed with scientific methods. During an empirical analysis based on a series of test games not all players should use their skill to win the game.
Main page: English, Deutsch
